



This test case is similar to 6.3 but with eccentric cylinders. While the concentric cylinders case can be reduced to a one-dimensional equation in polar coordinates (the radial velocity component vanishes), this is not the case for eccentric cylinders. For this problem (also known as "journal bearing" flow), an exact analytical solution in the limit of Stokes flows was obtained by Wannier using conformal mapping [46].
The result of a computation using embedded solid boundaries is illustrated in Figure 179. The inner cylinder is rotating while the outer cylinder is fixed. Note the weak recirculation in the top part of the gap.
Figure 180 illustrates the rate of convergence with spatial resolution toward the analytical solution of Wannier.
Figure 180: Convergence of the maximum and RMS errors on velocity magnitude toward the analytical solution. 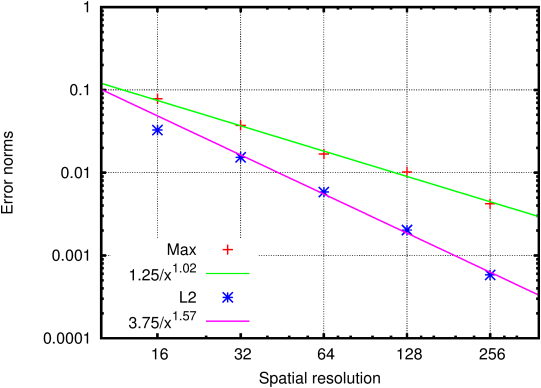
Same case as before but using bipolar coordinates to map the rectangular computational domain to the circular boundaries of the physical domain.
With these coordinates, solid embedded boundaries are not required and the number of grid points across the gap is constant (Figure 181). This markedly improves the convergence rate compared to the case using embedded solid boundaries (Figure 182).
Note also that this convergence can only be obtained when including the non-trivial viscous metric terms induced by the coordinate transformation.
Figure 182: Convergence of the maximum and RMS errors on velocity magnitude toward the analytical solution. 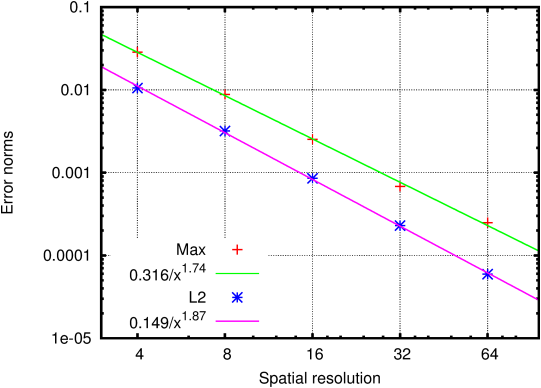
Here we test that the Wannier solution is recovered on a grid stretched in one direction. This validates the combination of stretched grids and embedded solid boundaries with Dirichlet conditions.
Figure 183: Convergence of the maximum and RMS errors on velocity magnitude toward the analytical solution. 


