PASS: Creeping Couette flow of Generalised Newtonian fluids

6.3 PASS: Creeping Couette flow of Generalised Newtonian fluids

Author: Stéphane Popinet
Command: sh couette.sh couette.gfs
Version: 1.0.0
Required files: couette.gfs (view) (download)
couette.sh profile prof-0.ref prof-1.ref prof-2.ref prof-3.ref
Running time: 38 seconds

Following [45], we solve for the 2D creeping flow between two coaxial cylinders. The inner cylinder rotates at a constant speed. The outer cylinder is fixed. The viscosity is a function of the second principal invariant of the shear strain rate tensor:

|D|=

√

∑

i,j

D_ijD_ij

where D_ij=(∂_iu_j+∂_ju_i)/2.

We use a general Herschel-Bulkley formulation of the form:

µ(|D|)=

τ_y

2|D|

+µ|D|^N−1,

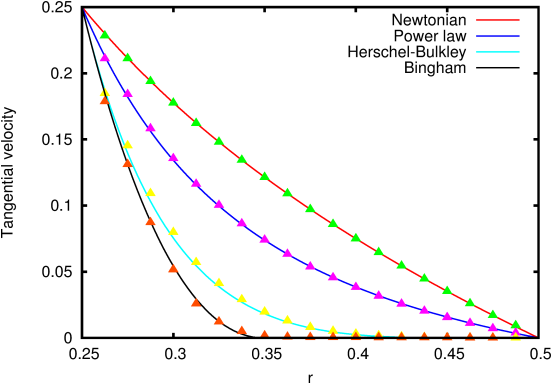
where τ_y is the yield stress. The solutions obtained for the stationary tangential velocity profiles for Newtonian, Power law (N=0.5), Herschel-Bulkley (µ=0.0672, τ_y=0.12, N=0.5) and Bingham (µ=1, τ_y=10, N=1) fluids are illustrated on Figure 91, together with the analytical solutions given by [7].

The Bingham fluid case is a particularly severe test of the diffusion solver, as the outer part of the fluid ring (r>0.35) behaves likes a rigid body attached to the outer boundary.

Figure 91: Tangential velocity as a function of radial position for various Generalised Newtonian fluids.