6.2 PASS:
Poiseuille flow
-
Author
- Stéphane Popinet
- Command
- sh poiseuille.sh poiseuille.gfs
- Version
- 100416
- Required files
- poiseuille.gfs (view) (download)
poiseuille.sh error.ref
- Running time
- 4 seconds
A simple parabolic Poiseuille flow in a periodic channel with a
constant along-channel acceleration a. The theoretical solution is given by:
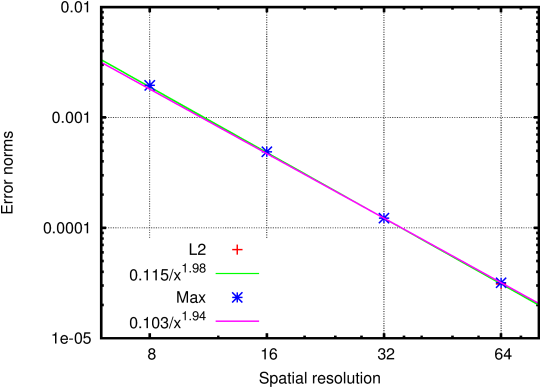
Figure 87 illustrates the norms of the error between
the computed and theoretical solutions as functions of spatial
resolution.
| Figure 87: Convergence of the error norms as functions
of resolution (number of grid points across the channel). |
6.2.1 PASS:
Poiseuille flow with metric
-
Author
- Stéphane Popinet
- Command
- sh ../poiseuille.sh metric.gfs
- Version
- 111025
- Required files
- metric.gfs (view) (download)
error.ref
- Running time
- 11 seconds
A simple Poiseuille flow but using a non-uniformly-stretch metric
across the channel.
Figure 88 illustrates the norms of the error between
the computed and theoretical solutions as functions of spatial
resolution.
| Figure 88: Convergence of the error norms as functions
of resolution (number of grid points across the channel). |
6.2.2 PASS:
Poiseuille flow with multilayer Saint-Venant
-
Author
- Stéphane Popinet
- Command
- sh river.sh river.gfs
- Version
- 120620
- Required files
- river.gfs (view) (download)
river.sh error.ref
- Running time
-
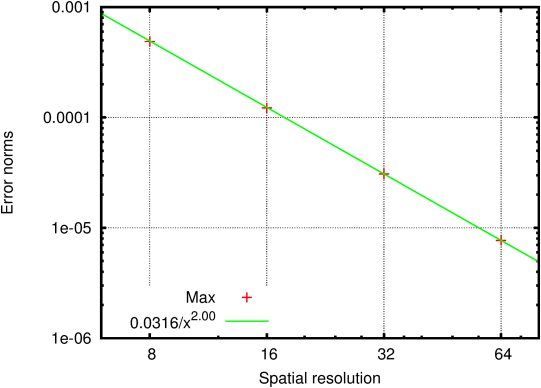
Similar test case but for a half-Poiseuille flow solved using the
multi-layer Saint-Venant solver.
| Figure 89: Convergence of the error norms as functions
of resolution (number of grid points in the channel depth). |
6.2.3 PASS:
Bagnold flow of a granular material
-
Author
- Pierre-Yves Lagrée
- Command
- sh ../poiseuille.sh bagnold.gfs
- Version
- 100416
- Required files
- bagnold.gfs (view) (download)
error.ref
- Running time
- 40 seconds
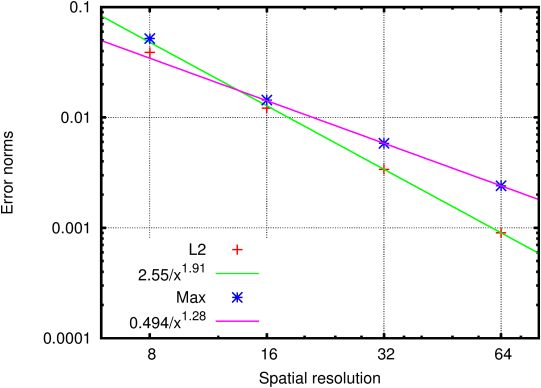
The flow of a granular material down an inclined plane is simulated
using a "µ(I)" rheology. The computed velocity profile is
compared with Bagnold’s theoretical solution.
Figure 90 illustrates the norms of the error between
the computed and theoretical solutions as functions of spatial
resolution.
| Figure 90: Convergence of the error norms as functions
of resolution (number of grid points across the channel). |