10.1 PASS:
Sessile drop
-
Author
- Stéphane Popinet
- Command
- sh sessile.sh
- Version
- 110912
- Required files
- sessile.gfs (view) (download)
sessile.sh error-6.ref
- Running time
- 3 minutes 57 seconds
A sessile drop is a drop of liquid at rest on a solid surface. In
the absence of gravity, the shape of the drop is controlled by
surface tension only. An important parameter is the "contact angle"
θ between the solid surface and the interface. In the absence
of gravity, the drop is hemispherical and it is easy to show that
the relation between the radius of the drop R and its volume V
is (for two-dimensional drops)
To test this relation, a drop is initialised as a half-disk
(i.e. the initial contact angle is 90∘) and the contact angle
is varied between 30 and 180∘. The drop oscillates and
eventually relaxes to its equilibrium position. This equilibrium is
exact to within machine accuracy (for most contact angles). The
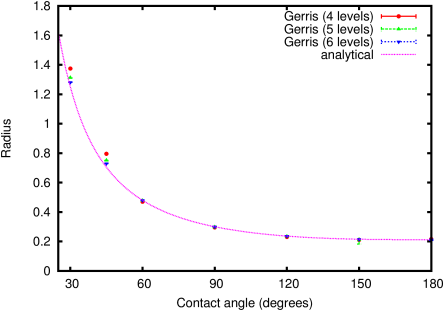
curvature along the interface is constant. Figure 126
illustrates the dependence of the equilibrium radius R as a
function of the contact angle θ (for a constant volume
V). The method is between first- and second-order accurate (Figure
127).
| Figure 126: Dependence of the equilibrium radius on the
contact angle for several spatial resolutions. |
| Figure 127: Convergence of the equilibrium curvature
with the spatial resolution. |