(a)  |
(b) 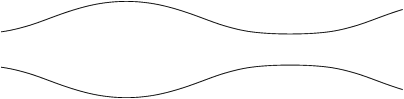 |
(c) 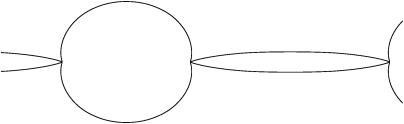 |
(d)  |



An inviscid cylinder of dense liquid is unstable under surface tension forces. The initial growth of the perturbation is described by the Rayleigh–Plateau linear stability theory. Close to pinchoff, non-linear effects cannot be neglected and fully non-linear solutions must be sought. Using simple similarity arguments, one can predict that the minimum radius of the deformed cylinder should tend toward zero as (t0−t)2/3 while the axial velocity should diverge as 1/(t0−t)1/3, with t0 the time of pinchoff.
This test case verifies that these scalings can be recovered using an axisymmetric VOF calculation.
Figure 122 illustrates the initial growth, pinchoff and satellite drop formation. The animation of Figure 123 shows how adaptivity is used to track the high curvatures and short timescales close to pinchoff. Up to 14 levels of refinement are used to capture roughly four orders of magnitude in characteristic spatial scales.
The scalings for the minimum radius and maximum velocity are given in Figures 124 and 125, together with the theoretical fits. The fit is excellent for at least three orders of magnitude in timescale. The departures from the power laws close to pinchoff are due to saturation of the spatial resolution (the minimum value on the y-axis of Figure 124 is the grid size 1/214).
See also [32], [34] and the 3D plateau example.
(a) (b) (c) (d)
Figure 123: Animation of a closeup view of the pinchoff area and adaptive mesh refinement. The colours correspond to spatial resolution. Dark red is 14 levels of refinement.


