13.1 PASS:
Circular dam break on a sphere
-
Author
- Stéphane Popinet
- Command
- gerris2D -m lonlat.gfs
- Version
- 090924
- Required files
- lonlat.gfs (view) (download)
isolines.gfv
- Running time
- 3 minutes 2 seconds
An initial circular cylinder collapses and creates shock and
rarefaction waves. The initial condition are radially-symmetric and
should remain so. The problem is discretised using
longitude-latitude spherical coordinates. Deviations from radial
symmetry are a measure of the accuracy of treatment of geometric
source terms.
This test case was proposed by [20], Figures 5 and 6.
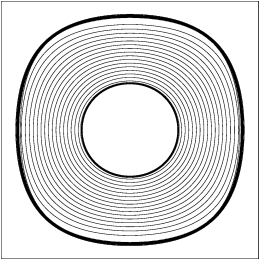
| Figure 156: Solution to the shallow-water equations computed on a
longitude-latitude grid in the domain
[−75∘,75∘]×[−75∘,75∘] with 256×
256 points. The solution is shown at times (a) t=0.3, (b)
t=0.6, and (c) t=0.9. The contours do not appear circular
because the solution has been projected down to a plane. |
| Figure 157: Scatter plot of the (radial) solution shown in Figure
156. The green line is the average solution. The solution
is shown at times (a) t=0.3, (b) t=0.6, and (c) t=0.9. |
13.1.1 PASS:
Circular dam break on a “cubed sphere”
-
Author
- Stéphane Popinet
- Command
- gerris2D -m cubed.gfs
- Version
- 120812
- Required files
- cubed.gfs (view) (download)
isolines.gfv
- Running time
- 8 minutes 24 seconds
Same test case but using a “cubed sphere” metric and adaptive mesh
refinement. There is noticeable distortion close to the cubed sphere
“poles” (Figures 158.(c) and 159.(c)).
| Figure 158: Solution to the shallow-water equations
computed on a “cubed sphere” with adaptive mesh refinement.
The solution is shown at times (a) t=0.3, (b)
t=0.6, (c) t=0.9, (d) t=1.2, and (e) t=1.5. The contours do
not appear circular because the solution has been projected down to
a plane. |
| Figure 159: Scatter plot of the (radial) solution shown in Figure
158. The green line is the average solution. The solution
is shown at times (a) t=0.3, (b) t=0.6, (c) t=0.9, (d)
t=1.2, and (e) t=1.5. |
13.1.2 PASS:
Circular dam break on a rotating sphere
-
Author
- Stéphane Popinet
- Command
- gerris2D -m coriolis.gfs
- Version
- 090924
- Required files
- coriolis.gfs (view) (download)
isolines.gfv
- Running time
- 5 minutes 56 seconds
Similar test case but with rotation. See also test case of [20], Figure 7.
| Figure 160: Solution to the rotating shallow-water equations computed
on a longitude-latitude grid in the domain
[−75∘,75∘]×[−75∘,75∘] with 256×
256 points. The Coriolis parameter is set to f=10. The solution
is shown at times (a) t=0.4, (b) t=0.8, and (c) t=1.2. |