


Von Kármán [22] showed that the steady flow of an incompressible liquid of kinematic viscosity ν induced by an infinite plane disk rotating at angular velocity Ω can be described by a similarity solution. In effect, using ζ=z√Ω/ν and setting the axial velocity U, radial velocity V and azimuthal velocity W as
| U= | √ |
| F(ζ) V=Ω r H(ζ) W = Ω r G(ζ) |
the Navier-Stokes equations reduce to a couple of ODEs:
| F‴−F F″ +F′2/2 +2G2 = 0 and G″−F G′+G F′ = 0 |
with boundary conditions
| F(0)=F′(0)=0 G(0)=1. and F′(∞)=G(∞)=0. |
where the prime denotes differentiation with respect to ζ.
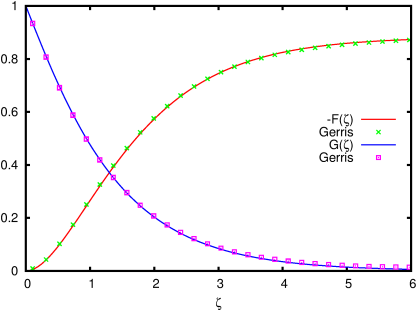
In figure 77 the analytical dimensionless axial and azimuthal velocities of Von Kármán are compared with the numerical solutions obtained with the axisymmetric solver including azimuthal velocity (swirl).


