9.1 PASS:
Circular droplet in equilibrium
-
Author
- Stéphane Popinet
- Command
- sh spurious.sh spurious.gfs 4e-10
- Version
- 1.1.2
- Required files
- spurious.gfs (view) (download)
spurious.sh convergence.ref kconvergence.ref
- Running time
- 6 minutes 46 seconds
A circular droplet of diameter D=0.8 is initialised centered on
the top-left corner of the unit box. Surface tension is imposed on
the interface. The exact solution is given by Laplace’s law: uniform
zero velocity and a pressure jump accross the interface exactly
balancing the surface tension force.
The initial condition – while close to the exact solution – does
not guarantee the exact balance between the numerical
discretisations of surface tension and pressure gradient. However,
these small initial perturbations generate small capillary waves
which are progressively (on a timescale of order D2/µ) damped
by viscosity so that the exact (to round-off error) balance is
eventually obtained.
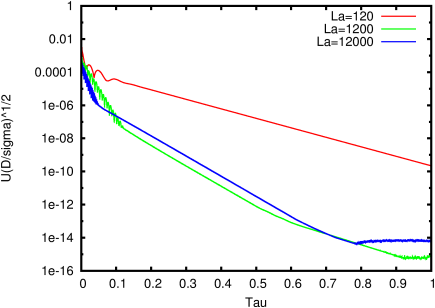
The convergence is obtained for a wide range of Laplace numbers
La=σρ D/µ2, as illustrated on Figure 106.
Correspondingly, convergence of the curvature to a constant value is
also obtained at all Laplace numbers as illustrated on Figure
107.
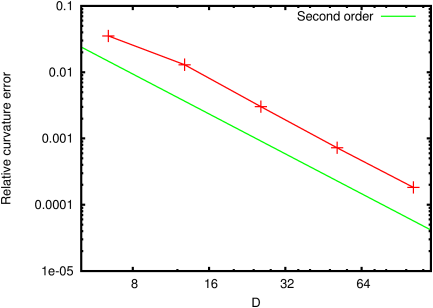
Figure 108 illustrates the convergence of the error on
the droplet shape as a function of resolution for a Laplace number
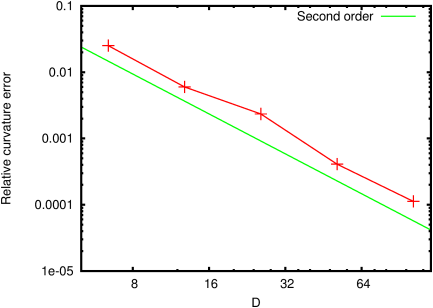
of 12000. Both the shape error and the relative error on the
equilibrium curvature value illustrated on Figure
109 show close to second-order convergence.
| Figure 106: Evolution of the amplitude of the capillary currents
max(|u|)(D/σ)1/2 as a function of
non-dimensional time τ=tµ/D2 for the range of Laplace
numbers indicated in the legend. |
| Figure 107: Evolution of the standard deviation of the
value of the curvature along the interface as a function of
non-dimensional time τ=tµ/D2 for the range of Laplace
numbers indicated in the legend. |
| Figure 108: Convergence of the error on the equilibrium shape of the
droplet with resolution. The diameter is given in number of grid
points. |
| Figure 109: Convergence of the relative error on the
equilibrium curvature value with resolution. The diameter is given
in number of grid points. |
9.1.1 PASS:
Axisymmetric spherical droplet in equilibrium
-
Author
- Stéphane Popinet
- Command
- sh ../spurious.sh axi.gfs 5e-8
- Version
- 1.3.1
- Required files
- axi.gfs (view) (download)
convergence.ref kconvergence.ref
- Running time
- 17 minutes 22 seconds
The same test case but using the axisymmetric solver. The results
are comparable.
| Figure 110: Evolution of the amplitude of the capillary currents
max(|u|)(D/σ)1/2 as a function of
non-dimensional time τ=tµ/D2 for the range of Laplace
numbers indicated in the legend. |
| Figure 111: Evolution of the standard deviation of the
value of the curvature along the interface as a function of
non-dimensional time τ=tµ/D2 for the range of Laplace
numbers indicated in the legend. |
| Figure 112: Convergence of the error on the equilibrium shape of the
droplet with resolution. The diameter is given in number of grid
points. |
| Figure 113: Convergence of the relative error on the
equilibrium curvature value with resolution. The diameter is given
in number of grid points. |