Analytical solutions for the damped oscillations of a liquid in a parabolic container have been derived by Sampson et al [40, 25]. Figure 139 illustrates the numerical and analytical solutions at t = 1500 seconds. Wetting and drying occur at the two moving contact points and hydrostatic balance is approached as time passes.
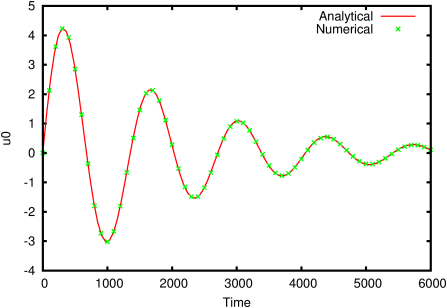
Figure 140 gives the analytical and numerical solutions for the horizontal component of velocity (which is spatially constant). Figures 141 and 142 give the relative errors in surface elevation and horizontal velocity respectively, as functions of spatial resolution.
The errors are small and larger-than-first-order convergence rates are obtained.
See also [33] for details.
Figure 140: Time evolution of the (spatially constant) horizontal velocity. Seven levels of refinement. 
Same test case but with a slightly-inclined, narrow channel defined using embedded solid boundaries.
See also [3] for details.
Figure 143: Time evolution of the (spatially constant) horizontal velocity. Seven levels of refinement.