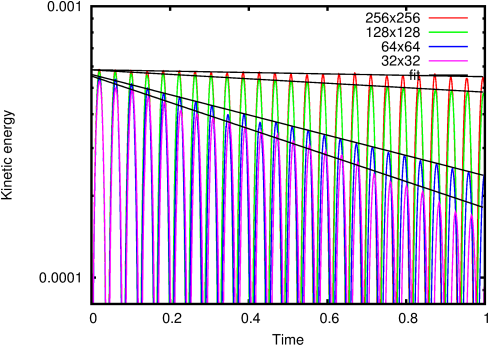
A two-dimensional elliptical droplet (density ratio 1/1000) is released in a large domain. Under the effect of surface-tension the shape of the droplet oscillates around its (circular) equilibrium shape. The fluids inside and outside the droplet are inviscid so ideally no damping of the oscillations should occur. As illustrated on Figure 119 some damping occurs in the simulation due to numerical dissipation.
This simulation is also a stringent test case of the accuracy of the surface tension representation as no explicit viscosity can damp eventual parasitic currents.
Figure 119: Evolution of the kinetic energy as a function of time for the spatial resolutions indicated in the legend. The black lines are fitted decreasing exponential functions. 
The initial shape of the droplet is given by:
| r(θ) = r0 + αcos(nθ) |
The oscillation frequency is then [43]:
| ωn2= |
|
A comparison between the theoretical and numerical values of the frequency is given in Figure 120.
The amount of numerical damping can be estimated by computing an equivalent viscosity. With viscosity, kinetic energy is expected to decrease as:
| exp(−Cν/D2t) |
where C is a constant, ν the viscosity and D the droplet diameter. Using curve fitting the damping coefficient b=Cν/D2 can be estimated (black curves on Figure 119). An equivalent Laplace number can then be computed as:
| La= |
| = |
|
The equivalent Laplace number depends on spatial resolution as illustrated in Figure 121.
