14.5 PASS:
Gouy-Chapman Debye layer
-
Author
- J.M. López-Herrera
- Command
- sh debye.sh
- Version
- 111123
- Required files
- debye.gfs (view) (download)
debye.sh points analytical
- Running time
- 12 seconds
The Debye layer is the ionic concentration and potential
distribution equilibrium structure that appears on the surface of a
charged electrode in contact with solvents in which are dissolved
ionic species. Gouy and Chapman proposed a model of a diffuse Debye
layer taking into account that the concentrations of these ionic
species are governed by the combined effect of its thermal diffusion
and its electrostatic attraction or repulsion.
In the case of a plane electrode within a fully dissolved binary
system (ion and counterions of valence z, |z|=1) the model
reduces to the following dimensionless equations:
| d2 φ/d x2 = −(n+−n−)=2 sinh(φ)
|
with the boundary conditions: φ(0)=φo and φ(x
→ ∞)=0. In the above equations the concentrations of
anions and cations, n+ and n− respectively, have been made
dimensionless with the bulk concentration, no, the potential
φ with (Kb T/e) and lengths with the Debye’s length
λD = [no e2/(Kb T ε)]1/2 where Kb is
Boltzmann’s constant, T the temperature, e the charge of the
electron and ε the permittivity of the fluid.
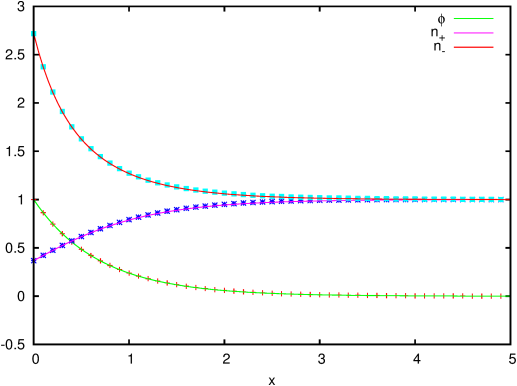
| Figure 211: Profiles of electric potential,
concentration of anions and cations in the Debye layer. The lines
are the analytical solution and the symbols the numerical
solution. |