


The wave model is used to reproduce the classical "Garden Sprinkler Effect" (GSE), a numerical artifact of the discrete directions of wave propagation (see Tolman, 2002).
A spatially-Gaussian wave spectrum is initialised in a 5000 km-squared domain. The other parameters are those of Tolman, 2002.
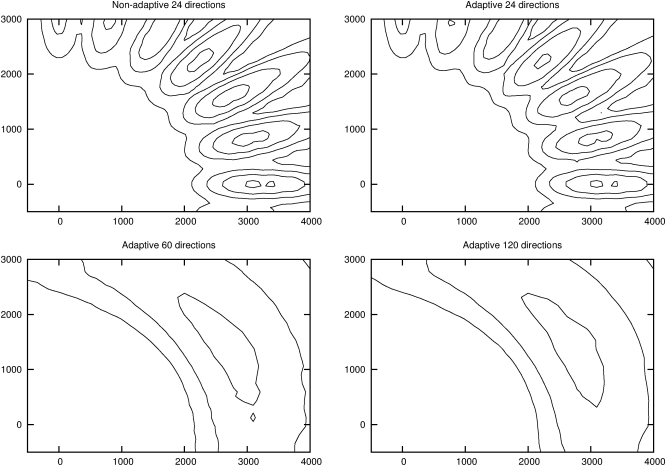
The final (t = 5 days) significant wave height for different model runs is illustrated in Figure 52. The interval between the isolines is 0.1 metres as in Figure 1 of Tolman, 2002. For a small number of discrete directions (24), the GSE is evident and the results closely match those of Tolman both for the constant resolution and the adaptive version of the code. For larger number of directions (60 and 120), the results do not show any obvious GSE and match the corresponding results of Tolman (Figure 1.b of Tolman, 2002 but note that the spatial resolution of Tolman is finer, 25 km rather than 78 km here).
The evolution in time of the significant wave height together with the corresponding adaptive discretisation is illustrated in Figure 53 for 120 directions. The mesh is adapted according to the spatial gradient in the significant wave height. This results in substantial savings in computational cost as illustrated by the timings given in Table 1. The computational cost with 120 directions is comparable to the cost with 24 directions on a regular (i.e. non-adaptive) mesh. This demonstrates that the GSE can be alleviated – at comparable computational cost – by combining adaptive refinement with a refined discretisation in direction space.
Table 1: CPU time for the four models of Figure 52.
Adaptivity # directions CPU time (seconds) No 24 582 Yes 24 179 Yes 60 312 Yes 120 699


