

This is one of the test cases presented in Popinet [31]. We solve the Poisson equation in a square domain with Dirichlet boundary conditions on all sides and the right-hand-side:
| ∇·U⋆⋆(x,y) = −π2(k2+l2)sin(π kx)sin(π ly) |
with k = l = 3. The exact solution of the Poisson equation with this source term is
| φ(x,y)=sin(π kx)sin(π ly). |
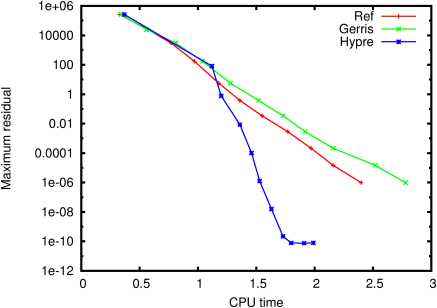
Figure 1 illustrates the evolution of the maximum residual as a function of CPU time. Figure 2 illustrates the average residual reduction factor (per V-cycle). The evolution of the norms of the error of the final solution as a function of resolution is illustrated on Figure 3. The corresponding order of convergence is given on Figure 4.
The curves labeled "Hypre" were obtained using the hypre module solver rather than Gerris’ built-in multilevel solver.
Same as the previous test but in order to test the accuracy of the gradient operator at coarse/fine boundaries, two levels of refinement are added in a circle centered on the origin and of radius 0.25.
The solver still shows second-order accuracy in all norms (Figure 8).
Similar to the previous test but with embedded solid boundaries and a non-trivial Dirichlet boundary condition. This test case was proposed by [21]. The boundary of the domain is defined by
| r < 0.30 + 0.15cos(6θ) |
The Poisson problem to solve in this domain is
| ∇2Φ=7r2cos(3θ) |
which has the exact solution
| Φ=r4cos(3θ) |
which is used as boundary condition.

