14.3 PASS:
Charge relaxation in an axisymmetric insulated conducting column
-
Author
- J.M. López-Herrera and S. Popinet
- Command
- sh cylinder.sh cylinder.gfs
- Version
- 100609
- Required files
- cylinder.gfs (view) (download)
cylinder.sh norms.ref
- Running time
- 5 seconds
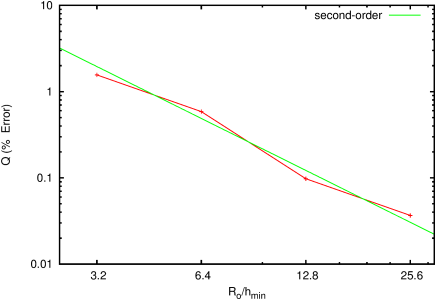
A conducting rigid cylinder of radius Ro=0.1 is immersed in an
insulating medium. Initially an uniform charge volume density is set
in the cylinder (ρe (x,0)=0.5). As time passes the
charge migrates from the bulk to the interface of the cylinder but
the total charge in the cylinder section is preserved.
| Q(t)= | ∫ | | ρe(x,t) d Σ = Qo= π Ro2 ρe(x,0).
|
If a VariableVOFConcentration is used instead of a VariableTracer
the total charge is also preserved. The outer electric field
reaches a steady-state (Figure 204).
A more detailed discussion of this simulation is given in
[26].
| Figure 203: Relative error on the
charge per unit of length of cylinder as a function of
resolution. (% Error =|1−Q(t)/Qo)|) |
| Figure 204: Steady-state electric field profile
as a function of resolution. |
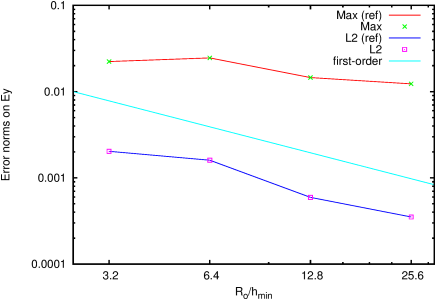
| Figure 205: Error norms for the electric field. |
14.3.1 PASS:
Charge relaxation in a planar cross-section
-
Author
- J.M. López-Herrera and S. Popinet
- Command
- sh ../cylinder.sh planar.gfs
- Version
- 100609
- Required files
- planar.gfs (view) (download)
norms.ref
- Running time
- 10 seconds
Same problem but solved in a planar cross-section of the column.
| Figure 206: Relative error on the
charge per unit of length of cylinder as a function of
resolution. (% Error =|1−Q(t)/Qo)|) |
| Figure 207: Steady-state electric field profile
as a function of resolution. |
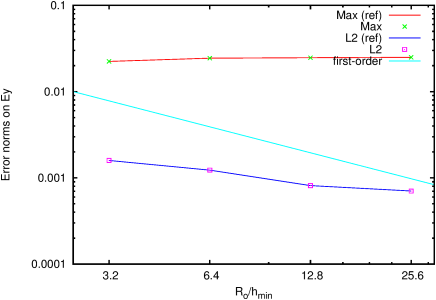
| Figure 208: Error norms for the electric field. |