 |  |
| t⋆=0 | t⋆=0.66 |
 |  |
| t⋆=0.95 | t⋆=1.24 |
 | |
| t⋆=1.52 | |
 | |
| t⋆=2.28 | |



Granular materials such as sand, rice, rocks etc... often exhibit “fluid-like” collective behaviour. It is thus tempting to try to describe the motion of granular matter using equations similar to those used to describe fluid motion (e.g. the Navier-Stokes equations). Things are not that simple however. The dissipative properties of granular matter are in particular quite different from those of simple fluids (i.e. Newtonian fluids which are characterised by a constant viscosity coefficient).
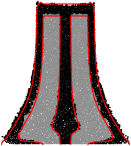
The search for constitutive equations (i.e. rheologies) able to describe flowing granular matter has been unsucessful for many years, so that the modelling of even simple granular flows (e.g. the flow of sand in an hourglass) was impossible up until very recently. In this example, we show how the recently proposed µ(I) rheology is able to describe very satisfactorily a complex granular flow: the collapse under its own weight of a column of grains. The aspect ratio of the column a is an important parameter and is set to 6.26 for this particular example. The animation in Figure 10 illustrates the evolution of the shape of the column as it collapses and spreads onto the horizontal surface (in black). The red line is a passive internal tracer which helps to visualise the deformation of the bulk.
Figure 11 compares the results of the continuum µ(I) model with a Contact Dynamics simulation [11] where the motion of individual grains is computed explicitly. The shapes of both the surface and bulk deformations are very well captured by the continuum model.
A detailed analysis of this example is given in [6].
t⋆=0 t⋆=0.66 t⋆=0.95 t⋆=1.24 t⋆=1.52 t⋆=2.28


